clip-pathで三角形を作成する方法は下記の記事で紹介しましたので、そちらを参照してください。
三角形に枠線をつけたい場面があるかと思いますが、clip-pathで作成した図形にborderで枠線をつけることはできません。borderでパパッとつけれたら楽なんですけど、残念ながらclip-pathは表示領域を作成するプロパティなため、borderを指定しても全然意図したように枠線がつけれません。そのため、clip-pathで作成した三角形に枠線をつけようとすると結構複雑です。
今回はclip-pathで作成した三角形に枠線をつける方法をご紹介します。CSSの解説パートでは数学が苦手ななないろによる数学の時間が始まります!
clip-pathで作成した三角形に枠線をつける
clip-pathで作成した三角形に枠線をつけるには工夫が必要です。基本的には二つの三角形を重ねて、前面側の三角形を背面側よりも小さくすることで枠線のように見せます。
正三角形に枠線をつける
clip-pathで作成した正三角形に枠線をつけてみましょう。div要素で枠線となる背面の三角形を作成し、疑似要素::beforeで前面にくる三角形を作成します。
See the Pen
三角形テスト by なないろ (@tflkhcei-the-vuer)
on CodePen.
<div class="equilateral_triangle_border"></div>.equilateral_triangle_border{
--w: 200px; /*背面にくる正三角形の横幅*/
position: relative;
width: var(--w);
clip-path: polygon(50% 0, 100% 100%, 0 100%);
aspect-ratio: 1 / cos(30deg);
background-color: #333; /*枠線の色*/
}
.equilateral_triangle_border::before{
--b: 5px; /*枠線の太さ*/
position: absolute;
display: block;
content: '';
bottom: var(--b);
left: 50%;
transform: translateX(-50%);
width: calc(var(--w) - calc(2 * var(--b) * sqrt(3)));
clip-path: polygon(50% 0, 100% 100%, 0 100%);
aspect-ratio: 1 / cos(30deg);
background-color: #add4f6; /*正三角形の色*/
}変数--wは正三角形の横幅で、変数--bが枠線の太さです(--wは枠線も含めた幅になります)。ここの値をお好きなように設定して、正三角形のサイズや枠線の太さを調節できます。上のCodePenでも数値を変えて確認できます。
三角形の向きを変えたい時は、rotate()を使って回転させるのが楽だと思います。
CSSの解説
CSSを詳しく解説していきます。解説していくのは.equilateral_triangle_border::beforeの下記の部分です。
width: calc(var(--w) - calc(2 * var(--b) * sqrt(3)));解説が不要な方は飛ばして大丈夫です。なお、数学サッパリのなないろが考えたものなので、もっと簡単な考え方や式がある可能性は大です。
aspect-ratio: 1 / cos(30deg);で正三角形になる解説は、この記事の冒頭でご紹介した記事を参照してください。ここでは割愛します。
例として、幅200pxの正三角形の内側に5pxの枠線をつける場合、前面にくる青い正三角形(::before要素で作る三角形)の幅はいくつになるかを考えてみましょう。幅200pxの正三角形に5pxの枠線がついた図のイメージはざっくりこんな感じです。
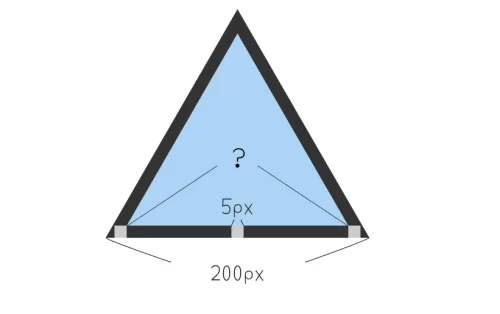
底辺に配置されているグレーの小さな四角は5px×5pxの正方形です。この図は実寸ではないので正確性には欠けますが、5pxの枠線をつけるからと言って、青い正三角形の横幅は単純に5px×2短くなるわけではないことはわかると思います。角度がついているからです。高さも同様に、5px×2短くなるわけではありません。
では、青い正三角形の横幅は一体どういう計算式で求めればいいのでしょうか?
背面の黒い正三角形の一辺の長さをwとし、枠線の太さをbとします。正三角形の各頂点から対辺に向かって垂線を引くと各頂点は二等分され、30°、60°、90°の直角三角形が6個できます。そのうちの1つ、下図の赤枠の部分の直角三角形に注目しましょう。赤枠の直角三角形の頂点をそれぞれA、B、Cとします。正三角形の頂点から垂線を引くと、対辺は二等分されるので、辺ACの長さは になります。
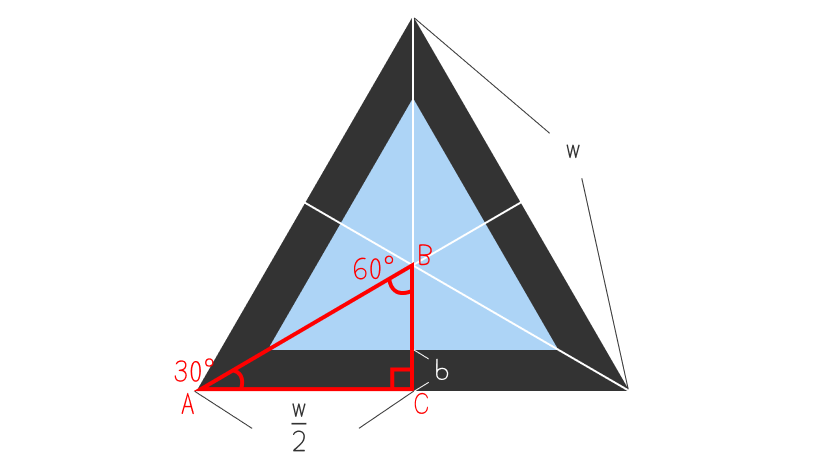
分かりやすいように赤枠三角形の部分を抜き出した下図で考えていきます。青い直角三角形の底辺と辺AB・辺BCとの交点をそれぞれD・Eとします。辺DEの長さは、求めたい青い正三角形の横幅の半分ですよね。つまり、辺DEの長さがわかれば青い正三角形の横幅もわかります。
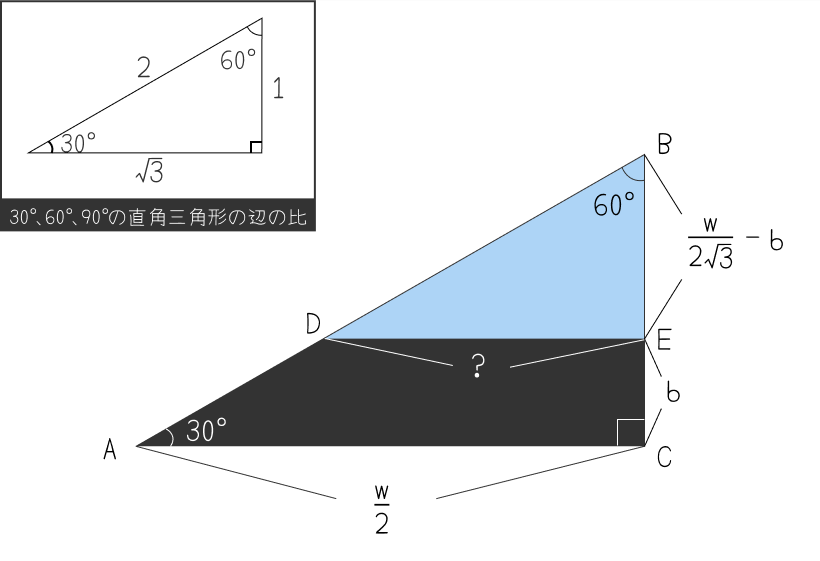
30°、60°、90°の直角三角形の辺の比は1:2:√3になることを利用して、辺DEの長さを求めていきます。まず、直角三角形ABCにおいて、辺AC = で、辺BCと辺ACの比が 1:√3であることから、
辺BC =
になります。ということは、辺BEは辺BCから枠線の太さであるbを引けば良いから、
辺BE =
になります。辺BEの長さが分かったので、青い直角三角形DBEでまた1:2:√3の比が使えます。辺BE = で、辺BEと辺DEの比が1:√3であることから、
辺DE =
になります。青い正三角形の幅は辺DEを2倍すればいいので、
青い正三角形の幅 =
ですね!上の式を計算して整理すると最終的にはこうなります。
青い正三角形の幅 =
この式を.equilateral_triangle_border::beforeのwidthに指定しています。 sqrt()は平方根を表す関数です。
width: calc(var(--w) - calc(2 * var(--b) * sqrt(3)));ちょっと()が多いしcalcがネストしててややこしく見えますが…。もっとすっきりさせたい場合は、√3を1.73にしちゃえば良いと思います。
width: calc(var(--w) - 2 * var(--b) * 1.73);同様に直角三角形を使って考えれば高さの計算式も出せますが、横幅が決まればaspect-ratio: 1 / cos(30deg);で正三角形の比率にできるので、高さの指定は省きました。
二等辺三角形に枠線をつける
clip-pathで作成した二等辺三角形に枠線をつけてみましょう。正三角形の時同様、div要素で枠線となる背面の三角形を作成し、疑似要素::beforeで前面にくる三角形を作成します。
See the Pen
clip-pathで作った三角形に枠線をつける by なないろ (@tflkhcei-the-vuer)
on CodePen.
<div class="triangle_border"></div>.triangle_border{
--w: 250px; /*背面にくる二等辺三角形の横幅*/
--h: 120px; /*背面にくる二等辺三角形の高さ*/
--b: 5px; /*枠線の太さ*/
--angle: atan2(var(--h), calc(var(--w) / 2));
--angle2: calc(var(--angle) / 2);
position: relative;
width: var(--w);
height: var(--h);
clip-path: polygon(50% 0, 100% 100%, 0 100%);
background-color: #333;
}
.triangle_border::before{
position: absolute;
display: block;
content: '';
bottom: var(--b);
left: 50%;
transform: translateX(-50%);
width: calc(var(--w) - 2 * var(--b) / tan(var(--angle2)));
height: calc((var(--w) / 2 - var(--b) / tan(var(--angle2))) * tan(var(--angle)));
clip-path: polygon(50% 0, 100% 100%, 0 100%);
background-color: #add4f6;
}変数が増え、正三角形よりややこしくなりました。もっと簡単なコードがある気しかしませんが、なないろが考えた結果はこうなりました。変数--wが二等辺三角形の横幅、変数--hが二等辺三角形の高さ、変数--bが枠線の太さです(--wと--hは枠線も含めた幅と高さになります)。変数--angleと--angle2は、--wと--hで指定した横幅と高さから計算された角度が入ります。--w、--h、--bの値をお好きに設定して二等辺三角形のサイズや枠線の太さを調節できます。
CSSの解説
二等辺三角形は二辺の長さが等しい三角形なので、幅と高さをいくつにしようと、この座標指定で二等辺三角形になります。
/*上向き三角形の場合*/
clip-path: polygon(50% 0, 100% 100%, 0 100%);
/*下向き三角形の場合*/
clip-path: polygon(0 0, 100% 0, 50% 100%);ただ、幅と高さによって二等辺三角形の形状は変化し、正三角形のように角度が決まっているわけではありません。角度は幅と高さによって決まるのです。下の3つはどれも二等辺三角形ですが、角度はバラバラですよね。二等辺三角形の性質として、二つの底角は等しくなり、頂角の二等分線は底辺を垂直に2等分します。
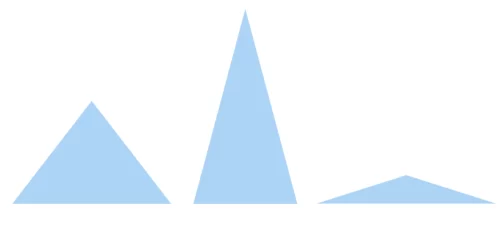
では、背面の黒い二等辺三角形の幅と高さがそれぞれw、hの時、前面に来る青い二等辺三角形の幅と高さがいくつになるのかを考えていきましょう。正三角形の時のような30°、60°、90°の直角三角形ができないので、1:2:√3の比が使えません。その分ややこしく見えますが、考え方は同じです。
背面に来る黒い二等辺三角形ABCの頂角から垂線を引き、底辺との交点をDとします。また、∠BACの二等分線を引き、辺BDとの交点をOとします。底辺AC = w、高さとなる辺BD = hですね。二等辺三角形の頂角から引いた垂線は底辺を二等分するので、辺AD = になります。
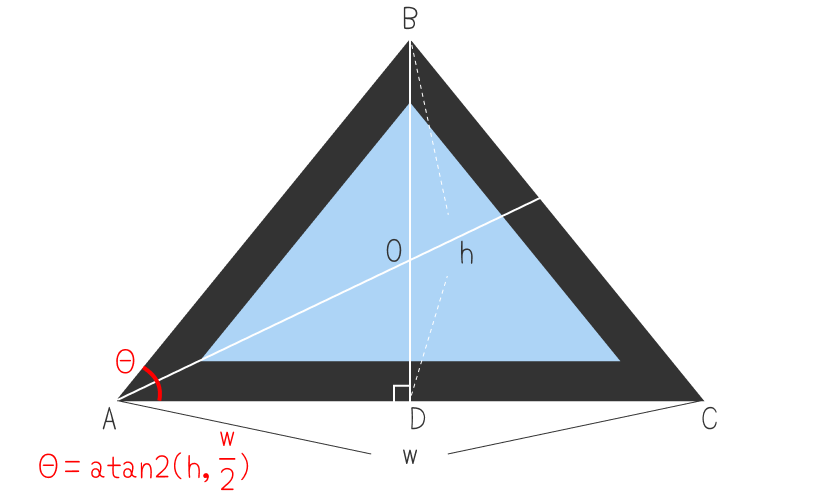
図で∠BACをΘとしていますが、これはCSSコードでは--angleという変数にしています。Θと変数--angleは同じで、角度のことです。三角形ABDは二等辺三角形を半分にした直角三角形で、tanΘが底辺(隣辺)ADと高さ(対辺)BDの比率になりますが、今はΘが何度かわかりません。このΘを求めるのに使うのが、逆三角関数の1つであるatan2()です。arctangent(アークタンジェント)のことです。
文系のなないろには逆三角関数なんて初耳でした。角度から底辺と高さの比率を求めるのがtanで、底辺と高さの比率から角度を求めるのがatan2だそうです。atanとatan2がありますが、2つの引数を取れるのがatan2で、今回はatan2を使っています。atan2(y,x)のように、カンマで引数を区切って使います。一般的にy座標(高さ)が先に来ます。Θを求めるためには直角三角形ABDにおける高さhと底辺 の比を使うので、
となります。
Θがわかったので、次は直角三角形AODを使って青い二等辺三角形の底辺がいくつになるか考えていきましょう。直角三角形AODの部分を抜き出すと下図のようになります。青い直角三角形の底辺と辺OA、辺ODとの交点をそれぞれE、Fとします。辺AD = 、辺FD = b ですよね。また、∠OADは∠BACの半分なので となります。 をCSSコードでは--angle2という変数にしています。
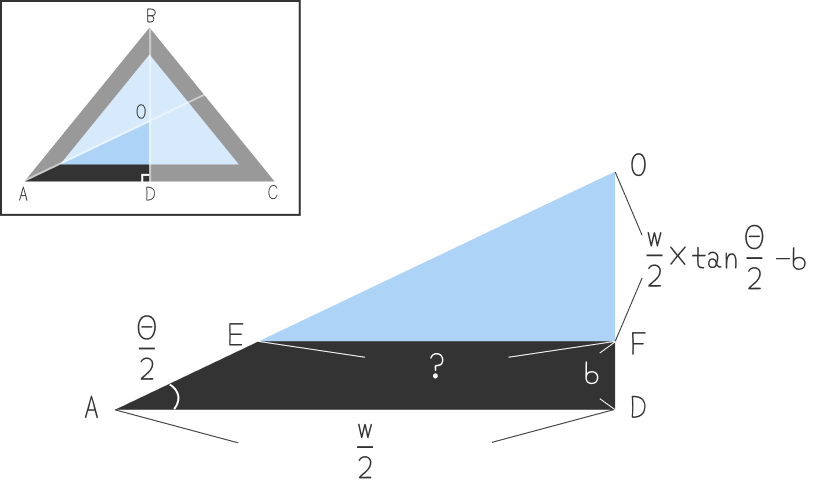
直角三角形において、tanΘ = になりますよね。この公式から、底辺か高さのどちらかがわかればもう一方を求めることができます。
これを利用するとまず辺ODの長さがわかります。辺ADにをかければよいですね。
辺OD =
ということは、青い直角三角形の高さである辺OFは、辺ODから枠線の太さ分引けば良いので
辺OF =
になります。青い直角三角形の高さがわかったので、底辺EFもわかりますね。辺OFをで割ればよいのです。
辺EF = =
辺EFは本来知りたい青い二等辺三角形の底辺の半分なので、青い二等辺三角形の底辺は辺EFを2倍すればいいわけです。
青い二等辺三角形の底辺 = =
これが最終的に.triangle_border::beforeの横幅に指定している式になっています。
width: calc(var(--w) - 2 * var(--b) / tan(var(--angle2)));青い二等辺三角形の底辺がわかったので、今度は高さを考えていきましょう。元々の二等辺三角形の頂角から垂線を引いてできた直角三角形ABDを使います。わかりやすいように直角三角形ABDの部分を抜き出したのが下の図です。青い直角三角形の頂点をそれぞれE、G、Fとします。∠BADがΘなので、∠GEFもΘになります。また、これまでの流れで辺EF = だと判明しています。
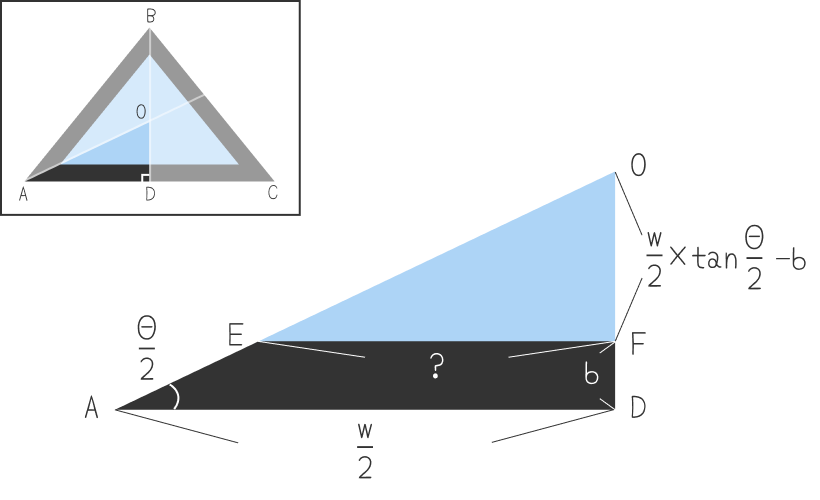
底辺と∠GEFがわかっているので、高さである辺GFが求められますね。
辺GF =
これが.triangle_border::beforeの高さに指定している式になっています。
height: calc((var(--w) / 2 - var(--b) / tan(var(--angle2))) * tan(var(--angle)));このように考えて、前面に来る二等辺三角形の幅と高さの設定をしました。
ジェネレーター
ジェネレーターを使いたい場合はこちらがおすすめです。clip-pathで作成する方法だけでなく、borderで作成する方法も選択できます。
こちらのジェネレーターがどのように幅と高さを計算しているかわかりませんが、なないろが作成したコードで出る数値と、こちらのジェネレーターが出す数値とを確認したところ、大きな違いはありませんでした。小数点以下の違いはありましたが…!
まとめ
clip-pathで作成した三角形に枠線をつけるのは結構難しいです。どうしてこういうコードになったのかを、数学が嫌い・苦手な人にもわかるようにお伝えしたかったのですが、なないろ自身が数学わかってないので、わかりにくかったり間違ってたらすみません。これでもかなり頑張って考えたのです。枠線自体はジェネレーターやコピペで簡単につけれますが、どうしてこうなるんだろうな~って疑問に思う方の助けになれば幸いです。
もっと複雑な図形、例えば星型とかに枠線をつけたいならsvgの方が簡単だと思います。
そして、HTMLで分数や数式を表現するのって結構面倒くさいってことを初めて知りました。MathMLを使ってみましたが、ややこしいですね。





